相乗平均(幾何平均)
ここで平均値をさらに深堀していきましょう。代表値のひとつでもある平均値ですが、相加平均の他にも異なる平均値があります。
まずは相乗(そうじょう)平均について学習してきましょう。幾何(きか)平均とも呼んだりしていて、言葉は2つありますがどちらも一緒です。
この記事で学習できること
- 相乗平均(幾何平均)
- 平均成長率
こちらの講座記事では、相乗平均と統一して記載してまいります。

これは事例を見ながら学習してきましょう。終わり良ければすべて良しという平均値が相乗平均だよ!
第9講座
売上パフォーマンスなどの成果レポートを眺めていると、誤った計算式を使っているシーンに遭遇します。
例えば、以下のような売上を想定してください。
| 日付 | 売上 |
| 2020年3月 | 1,000万円 |
| 2021年3月 | 1,200万円 |
| 2022年3月 | 980万円 |
| 2023年3月 | 1,300万円 |
| 2024年3月 | 1,400万円(見込み) |
最新の売上見込みと、2020年3月と比較して「1,400÷1,000 = 140%増」になった、といった計算式を多く目にしました。
これは一見正しく思えますが、実は誤りです。
2020年と比較する場合、2021年~2023年の実績が喪失してしまっています。この間の年月があって今があるわけですから、ピンポイントで2020年と比較してしまうと、意味が異なってしまうのです。
時間は連続しています。2020年の終わりから、タイムマシーンで2023年にやってきてそこから1年頑張った! という意味合いとなってしまうわけです。
この場合、相乗(そうじょう)平均という計算式を使って、平均成長率を算出します。まずは、相乗平均について学習をしてまいりましょう。
相乗平均とは?
これは、一連の数値の積の n乗根 として定義される特殊な平均値です。ここで n は数値の個数を表しています。
相乗平均 =( a₁ × a₂ × a₃ × … a(n) ) の 1/n乗
計算方法は2種類あり、① 直接の金額で算出する方法と、② 前年比率で算出する方法と2通りあります。この記事で求める平均成長率は②の算出方法となりますが、ひとまずそれぞれの使い分けを見ていきましょう。
① 実際のデータで相乗平均を求めるケース
まず、5年分のデータを使って相乗平均を算出します。
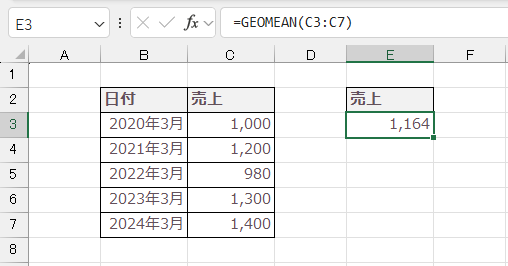
実際のデータを使うと(1,000×1,200×980×1,300×1,400)の1/5乗が答えとなります。Excelを使用して計算すると「約1,164万円」となります。
GEOMEAN(ジオ・ミーン)関数で、AVERAGE関数と同じような使い方で結果を求めることが可能です。
これは2020年から2024年度までの平均的な売上の成長を表した値となります。
初年度は1,000万円の売上からスタート。
アップダウンはあったけれども、初年度から平均して+約1,164万円の売上で平均的に成長している、と評価する見方となります。
こちらは直感的な値として、売上の成長具合をデータから読むことができます。
注意点として、毎年約1,164万円ずつプラスだ! という意味ではないこと抑えておいてください。学校の通知表のような評価値であり、実データと混合してはいけません。
特に、初年度の1,000万円と割り算して、約16%増であるという表現も間違いです。
この計算をしてしまうことで、次にご紹介する前年比で相乗平均を求めるケースとごっちゃになり、混乱してしまうケースが多いのでご注意ください。
前年比で相乗平均を求めるケース
各データの前年比率を求めると、次の通りです。
- 2021年:120% → 1.20
- 2022年:82% → 0.82
- 2023年:133% → 1.33
- 2024年:108% → 1.08
各前年比の割合(1.2×0.82×1.33×1.08)の1/4乗で求めると、答えは「約1.09」が算出されます。
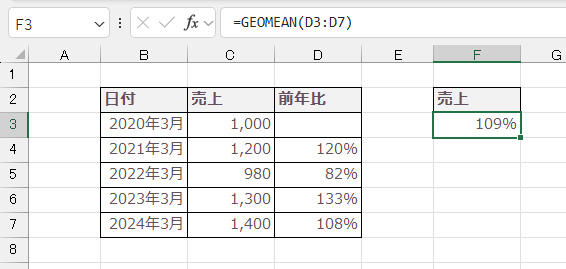
2020年から2024年まで約9%ずつの成長をした、と見ることができます。
この値が平均成長率です。
割合で見るため、全体を把握しやすい値として表現することができます。異なる部門の成長率を見比べるときなどは、こちらの計算方法が有効です。
ただし、算出結果は割合を使っているため、①のような絶対的な数値データで見ることはできません。
どちらを扱うべきか?
実際のデータを使用して直接相乗平均を計算する方法と、前年比の割合を用いて相乗平均を計算する方法には、それぞれ利点と制限があります。
- 実データでの相乗平均
- 年間の売上や利益などの実際の数値に基づいて、平均成長金額を計算します。
- このアプローチは、実際の金額の変動を直接反映しますが、年間の変動が大きい場合、結果が歪むことがあります。
- 成長率(割合)での相乗平均
- 各年の前年比を計算し、その割合の相乗平均を求めます。
- このアプローチは、成長の割合の均一性をよりよく反映する可能性があります。特に、年間の成長が不均等な場合に有効です。
以上の違いがあります。実際には②の計算式のほうがわかりやすいし、伝わりやすいというメリットがあるため、一般的な計算方法と言えるでしょう。
しかし、最新の売上年度が初年度を下回った場合、②の算出方法では成長率が100%を下回る計算結果となってしまいます。
②の計算方法は、初年度と最終の値で平均成長率が算出される計算式のため、終わり良ければすべてよし、と見える値でもあり、そこが難点です。
| 日付 | 売上 |
| 2020年3月 | 1,000万円 |
| 2021年3月 | 1,200万円 |
| 2022年3月 | 980万円 |
| 2023年3月 | 1,300万円 |
| 2024年3月 | 600万円(見込み) |
- 実データの計算結果では「約983万円」
- 前年比の計算結果では「約88%」
実際に計算をすると、この表現の差が出ます。
途中経過がよくても、最新の業績が悪いと平均成長率88%となり、企業はマイナス成長であるという印象が伝わってしまいます。
①の場合は実測データの掛け算をしてデータを掛け合わせるため、最新の売上年度が低くても、大きなマイナス表現にはなりません。
しかし、一般的に100%を下回ったとしても、②の計算方法で平均成長率を出すほうがシンプルなので、一般的には②の計算方法で数値を追うことをおすすめします。
①の計算式は、現場内のステータス確認のみの利用でいいかと考えています。
第三者に伝えるときは、現場の売上を教えられても業種・業界によって規模が不明瞭なので、割合のほうが伝えやすいですからね。
毎年どれくらいの成長か減衰かよりも、損益分岐点さえ下回っていなければとりあえずOKなのですから。
普通の平均値じゃダメなの?
合計÷個数で求められる平均値は、相加(そうか)平均と呼びます。
普通の平均値、つまり相加平均では(1,000+1,200+980+1,300+1,400)÷ 5 の計算式となり、「約1,176万円」となります。
この程度のデータであれば、相乗平均の値「約1,164万円」とさほど差が出ないのですが、どうして相加平均を使ってはいけないのでしょうか?
それは、現時点を終了地点とするか、継続地点とするかによって考え方が変わります。
もし、このビジネスが2024年で終了であれば、相加平均を採用します。これ以上、次年度は不要なので、合計÷継続した年数で構わないからです。
次年度も考慮した場合は、合計値ではなく各月の積の情報を重視します。
平均値では、外れ値を含む場合、外れ値によって平均値が引っ張られてしまいますが、積の場合は外れ値を平滑化することができます。つまり、平均値を穏やかにさせて次年度に挑むといった側面がある、という認識で間違いないと思います。
そのため、結果は常に「平均値 > 相乗平均」になるということを抑えておいてください。
まとめ
次年度の目標値を設定することは、どの企業でもあるかと思います。目標なくして企業の成長はありませんからね。
その場合は、①と②の計算式で算出される範囲の値で設定するといいでしょう。2024年3月の売り上げが最初の見込みどおり、1,400万円で着地した場合、2025年度の目標値を考えてみましょう。
①の計算の場合、シンプルに約1,164万円以上の目標を設定をすればいいだけです。
②の計算式では、平均成長率が約1.09だったので、1,400万円×1.09 = 1,526万円の目標値を設定すればいいということになります。
つまり、約1,164万円~1,526万円のレンジが、売上目標の参考値となります。
その年度に、様々な情勢があると思いますが、この範囲内に収まる値を最低ラインとして設定してください。もちろん、損益分岐点は確実に超えているという点を考慮して設定してください。損益分岐を超えていなければ、そもそも終わりのビジネスですからね。
以上が相乗平均でした。

相乗平均を覚えるだけで、経営者目線でビジネスを俯瞰することができると思います。ぜひ覚えておいてください。



