統計学の最初のハードル「標準偏差」

①平均値、②中央値、③最頻値、④最大値、⑤最小値、⑥レンジと学習しました。

次に、基本統計量の中でも少し難しいと感じるかもしれない値、⑦分散、⑧標準偏差を学習していきましょう。

標準偏差は、特に①平均値をサポートする値として使われます。

それでは、説明にいきましょう！

この記事は長いので、時間のあるときにゆっくり熟読してね！

第4講座

平均値は、平らに均されている値であるため、ピンポイントの値でしかわかりません。均してしまったため、どんな姿をしたデータだったか、失われてしまっています。

そこで、平に均す前の状況を評価してくれるのが、標準偏差です。わかりやすいように、飲み会のシーンを例にしてみましょう。

標準偏差は、データが平均値からどれくらい離れているかを示す値だと思ってください。この値を「ばらつき」と表現していきます。

例えば、10人が参加した飲み会で、お会計が１人当たり6,000円だったとします。標準偏差の値が300円としたら、おおむね10人の飲食代は均等だったと評価できます。

では、標準偏差が1,500円だとしたらどうでしょう？

このようにばらつき具合が大きくなると、得をした人と損をした人と二分していると考えることができます。

お酒を飲んで、何回もお代わりした人と、ソフトドリンク２杯だけ頼んだ人の差をイメージしてください。そういった出来事が含まれていると想定できうる値です。

割り勘のような平均値は、すべての情報が平らに均されてしまうため、どういう内訳になっていたのかがわからなくなります。

そこで、この平均値のプラスマイナスのばらつきを教えてくれるのが、標準偏差という値です。つまり、平均値のサポート役というわけですね。

300円と1,500円の値の違い、感覚を、しっかりとこの記事で確認していきましょう。

標準偏差は、統計学で非常に重要な値です。この記事を通じて、標準偏差をしっかりと理解できるよう、頑張っていきましょう！

標準偏差の範囲は、約68％のデータが集まる！？

標準偏差は不思議な値で、平均値のブレ幅を教えてくれるだけではなく、その範囲内に全体の約68％のデータが集まるよ！　ということも教えてくれます。

先ほどの例で説明を続けると、平均値6,000、標準偏差300ということは、5,700～6,300の間に約68％のデータが集中している、と考えられます。

標準偏差が1,500だったら、4,500～7,500の間に約68％のデータが集中していると考えられます。そのため、データがばらついている（飲んだ人と飲まなかった人の幅が大きい）と考えられるわけです。

もちろん、すべてのシチュエーションで毎回必ず68％内に収まるというわけではなく、これは統計学上の一般的な目安となります。

世の中の不確かなことは正規分布に従うのだ、と仮定して物事を分析したほうが早いため、この68％暫定ルールを採用しています。

正規分布については、次に記載しますね。

標準偏差のプラスマイナスの範囲のことを１シグマといい、ギリシャ文字の「Σ」の小文字、「σ」を使って、１σと記載します。

プラスマイナスなので 「±１σ」 と表現します。

平均値6,000、標準偏差300とすると、5,700～6,300が、±１σの範囲となります。また、標準偏差を英語読みで読む機会も多いので、ここで合わせて覚えておきましょう。

標準偏差　＝　Standard Deviation（スタンダード・ディービエーション）といい、アルファベット２文字の「sd」という略語を使います。

平均値は「ave」と略されることがあり、PowerPointのようなスライドに平均値と標準偏差を合わせて記載するシーンがあったら、「ave±sd」と記載することもあります。

こちらも覚えておくといいでしょう。

正規分布について

続いて、正規分布について学習をしましょう。

正規分布という概念は、アブラーム・ド・モアブルによって1733年に導入をされ、

• ピエール・シモン・ラプラス
• アドリアン・マリ・ルジャンドル
• カール・フリードリヒ・ガウス

と、数多くの数学者が拡張していきました。正規分布という名前がついたのは19世紀ごろなので、一部不明瞭な解説となりますが、

• チャールズ・サンダース・パース
• フランシス・ゴルトン
• ヴィルヘルム・レキシス

によって、現在の正規分布に完成していったことは間違いありません。

つまり、アブラーム・ド・モアブルの初期導入から100年以上も数学の研究が続いて、ようやく現代の形になっていったわけですね。

世の中の不確かなものは、正規分布に従うのだ。

さて、正規分布というのは以下のキャプチャのように、釣鐘状をした曲線のことを指していますが、これはどのような意味を持っているのでしょうか？

実例として、平成27年の男子高校生の身長データを見てみましょう。

以下のキャプチャは、統計局から持ってきたデータをエクセルのVBAを使って加工し、グラフ化しました。釣鐘状の波形が見えてきますよね。

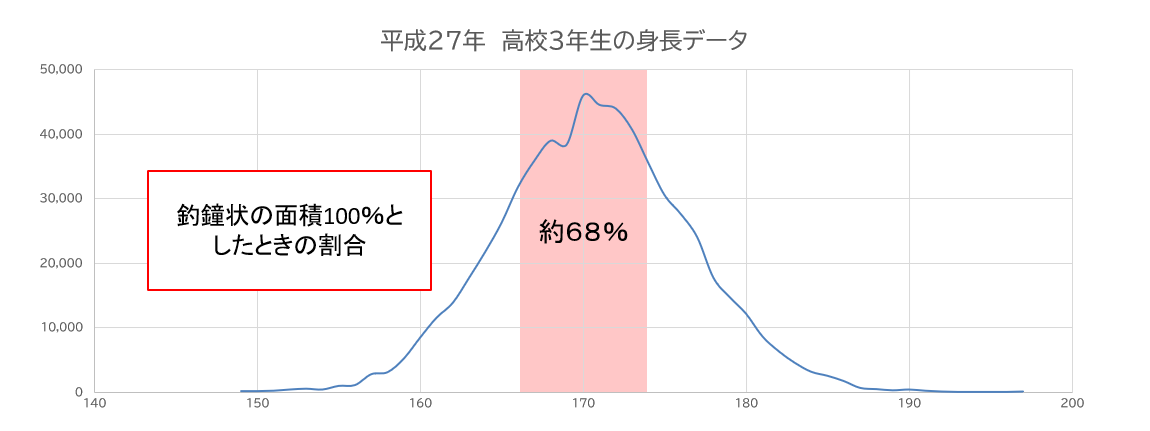
ちょっと形は欠けているとはいえ、立派に釣鐘状をした形となっています。

平均身長は171.3cm、標準偏差は5.8cmという計算結果になりました（統計局のデータは常にアップデートされているため、計算しなおすと若干のズレはあるかもしれません）。

つまり、165.5cm ～ 177.1cmの人の割合が、全体の約68％だということになります。

このように、世の中の不確かなことを実際に時間とお金をかけて調べてみると、若干のズレはあれど、正規分布に近づくことが数学者によって発見されたのです。

こういう情報があると、手元のデータの平均値と標準偏差さえわかれば、だいたいのデータ分布像を予測することができます。身長の例でいえば、洋服のサイズの生産バランスなども設計することができますよね。

そのため、統計学では正規分布に従うことを前提として、基本統計量に含まれる代表値を見ていくわけです。

私のExcel講座も、地球上にいるすべての人たちに指導するとしたら、どのようなレビュー結果となるでしょうか？

５段階評価としたら、どんなに努力をして素晴らしい講座ができたとしても、平均レビューポイントは「３」に収束する、ということになります。

学びが必要な人、そうでない人、そうでないけれども必要だと感じた人、やっぱり不要だった人、ものすごく満足を得た人、まったくわからなかった人、きれいな釣鐘状になることでしょう。これが正規分布というものです。

人間関係でも同じというマインドで私はいます。

自分と気の合う人と気の合わない人も、同じ割合でいるという考えでいると、実際にストレスの溜まる人と遭遇したとき、気分がずっと楽になるはずです。

講師業を始めた初期段階では、自分の指導は誰からでも受け入れられたいと思っていました。常にレビューは★５であるべきだ。ただ、それは疲れるだけでした。

以下、昔の自分へのメッセージとして。

人生で出会うすべての人が、自分に対して常に好意的ではありません。誰からも好かれたいと考えていたら、この正規分布を頭の中に入れると、とても気持ちが楽になるはずです。

⑦分散、⑧標準偏差

標準偏差の求め方は、Excelやプログラムを使うと一瞬で求めることができるのですが、この計算式は確実に覚えておきたい内容です。

長いですよね。それぞれの計算フローをExcelのキャプチャを使って解説していきます。ゆっくりとキャプチャを追っていってください。

データ群の平均値を求める

標準偏差を出力する最初の手順です。データ群の「平均値」を出力します。

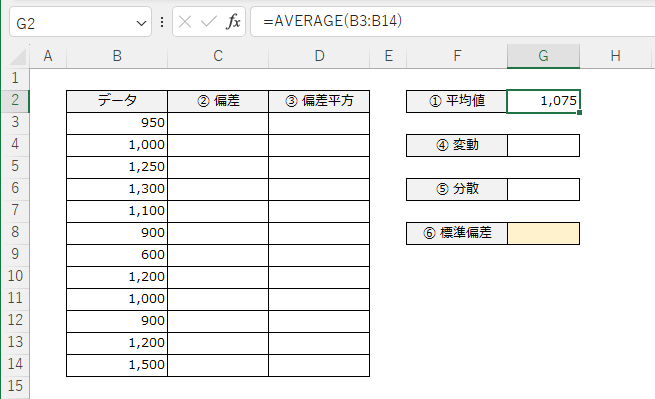
各データより「実データ – 平均値」で偏差を求める

平均からの距離を求めていきます。この値を「偏差（へんさ）」といいます。

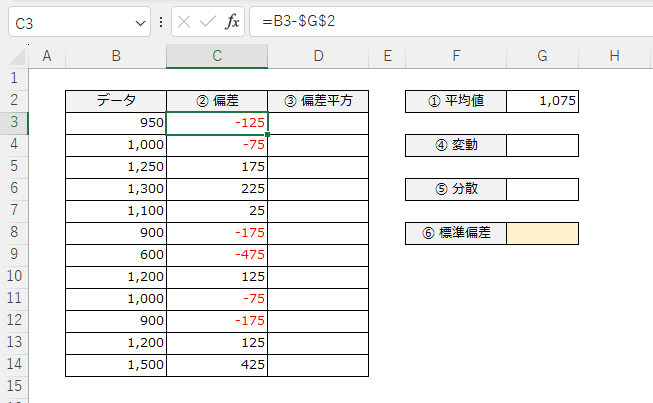
偏差を２乗して、偏差平方を求める

この偏差の平均値を求めれば、データのばらつきを求めることができるのですが、プラス方向の偏差と、マイナス方向の偏差の値がそれぞれ打ち消しあってしまい、合計値が０になってしまいます。

偏差の合計は０になるという性質があるため、これ以上の分析ができなくなってしまうのです。平均値が平らに均された値ゆえに、こうなってしまうのです。

では、偏差のデータを生かしたまま負の数を取り除くためにはどうしたらいいか？

数学者たちは絶対値にすればいいという案と、偏差を２乗して負の数を取り払えばいいという案が出ました。

実際に検証した結果、絶対値では散らばり度合いが大きくても小さく表示されてしまうため、偏差を２乗して負の数を取り払う案を採用しました。

そのため、偏差を２乗する、偏差平方を求めるというのが正解だと導いたわけです。

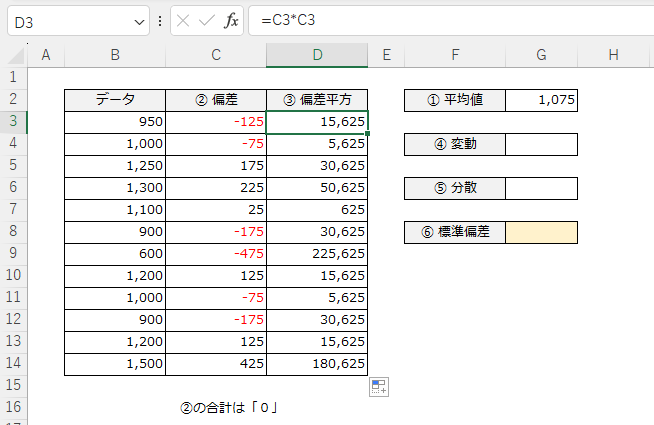
偏差平方の合計値を求めて、変動を出力する

平方偏差によって、負の数が取り除かれました。この合計値はかなり大きくなってしまうのですが、この偏差平方の合計値を「変動（へんどう）」といいます。

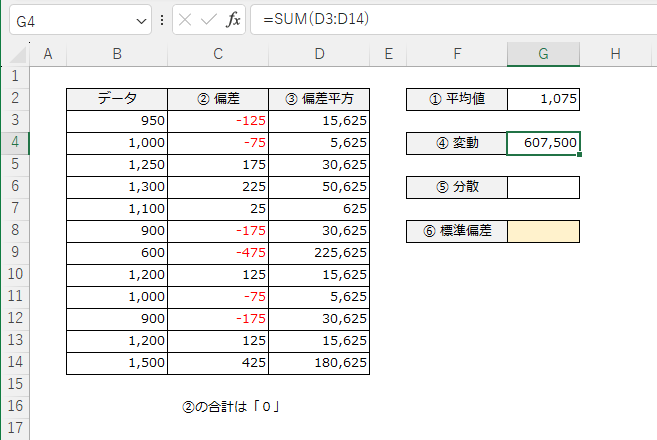
変動は基本統計量の代表値には含まれません。扱いづらい値ですからね。

変動をデータの個数で割り、⑦分散を求める

偏差の平均値を求めたかったのですから、変動をデータの個数で割ることで、分散を求める計算になります。偏差のデータの性質を維持したまま、データを打ち消しあうことなく平均値を求めることができます。

これが、データの散らばり具合を示す「⑦分散」という値になります（※ キャプチャ内は手順を示した番号のため、「⑤ 分散」となっています）。

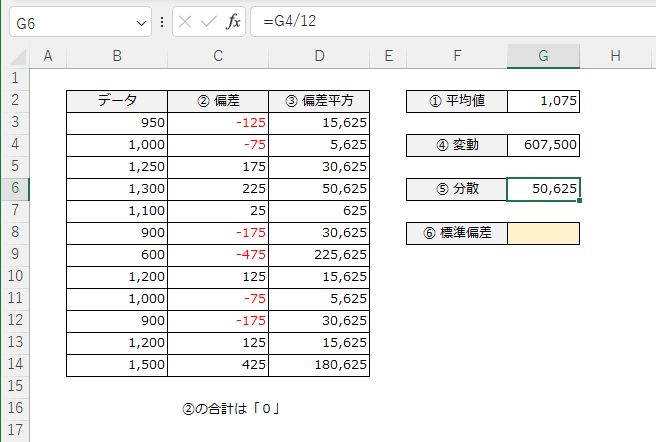
ただし、偏差平方のときに２乗してしまっているので、単位が変わってしまい、馴染みのない値になってしまっています。

単位が変わった？　ここがつまづきポイントです。

説明として、10ｍ×10mであれば、100m² という値になり、これは広さの値として私たちの利用できる単位となっています。

10円×10円をした場合、100円² という値になります。そのため、出現した値は普段利用しない単位の数値データとなるため、分散が出力されても私たちは読み取れないのです。

単位が異なるために、数字が読み取れないことを「スケールが異なる」と表現します。せっかくデータの散らばりを求めることができたのに、少し困りますよね。

分散の値を平方根にして、標準偏差を求める

読みやすい値に変換するため、２乗したから最後にその逆をやればいい。

√分散　→　標準偏差

つまり、この分散の値を平方根で戻します。「円²」を「円」に戻してあげる。ここではじめて元の単位に変換できたので、平均値からの ±1σ の距離を知ることができました。

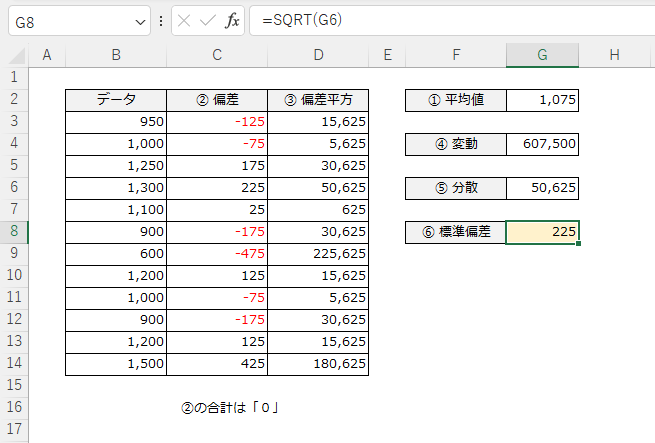
キャプチャの例では「1,075 ± 225（ave ± sd）」となります。

この範囲に68％のデータが集まる。

つまり標準偏差内で、それくらいのばらつきはあるだろう。これを上回るようであれば、平均から大きくズレているので、どのようなデータか確認する必要があるよね。

そんな気づきを得ることができます。

まとめ

以上が、⑦分散と⑧標準偏差でした。

ただ、まだここまでの理解では不十分です。いまご紹介した標準偏差の求め方は、母集団に対する計算方法、つまり手元に必要なデータがすべて揃ったときに使える計算方法だということです。

一般的にデータ分析をする際には、すべてのデータを集めることは不可能に近い。

時間とお金がかかりますし、集計期間中にデータが集まったとしても、データは時間とともに動くので、集まったデータからまた揺らいでいきます。

そのため、標本データ（サンプル）を使うことの方がほとんどです。違いは、分散の求め方となるのですが、この分散の求め方はまた別の機会にご紹介します。

まずは標準偏差の基本的な計算方法をしっかりと覚えておきましょう！　統計学の基礎中の基礎なので、これを知らないと話にならないくらいの内容ですね。

この記事はここまでです。次の記事は母集団と標本 – 標本の抽出方法に進んでください。

榊 裕次郎

Excel講師

1981年10月生まれのてんびん座、東京都出身。趣味は、旅行と料理とワイン。2024年は、佐賀県に行って「呼子のイカ」を思いっきり食べたいです。

引き続き、青森・秋田・岩手でのお仕事ご依頼、お待ちしております！