相関について
統計学が魅力的に思えたのは、この相関を学習してからです。この記事では、相関について学習をしていきましょう。
この記事で学習できること
- 相関とは?
- 相関係数について
- 相関係数の求め方
- 相関係数の読み方
人類・遺伝学における相関の発見
相対する2つの関係性、これを相関(そうかん)と呼びます。相関という概念は、イギリスの人類学者フランシス・ゴルトンによって、初めて提唱されました。
ゴルトンさんは研究する遺伝学の中において、「平均回帰」という現象を発見します。この現象を、人間の身長を例に見てみましょう。
- 高身長のお父さんの場合、息子は通常、お父さんより低い身長になりますが、平均身長よりは高くなる傾向にある。
- 低身長のお父さんの場合、息子の身長はお父さんより高くなりますが、平均身長よりは低い傾向にある。
- お父さんの身長が平均の場合、子供の身長も平均に近くなる。
私の父は日本人の平均身長に近い170cm、私は172cmで成長は止まりました。気にもしなかったのですが、皆さんはどうでしょうか? あてはまる方、いらっしゃいますか?
ゴルトンさんが発見した平均回帰から、2つの関係性の度合いを示す「相関係数」という概念が生まれました。
そして、彼の教え子であるカール・ピアソンや、ロナルド・フィッシャーは、統計学の計算式をさらに進化・発展させていきます。特に、教え子のカール・ピアソンは、ゴルトンさんが生んだ相関係数を、具体的な計算式で一般化しました。
ピアソンの積率相関係数というのは、現代でも扱われている相関係数です。ゴルトンさんの影響力の大きさは、本当にすごいですよね。
外部リンクで、総務省統計局が提供する「データサイエンス・スクール 統計力向上サイト」の「未来がわかる方程式」が面白かったので、参考リンクを貼っておきます。
未来がわかる方程式 – データサイエンス・スクール・統計力向上サイト
相関係数について
相関係数は、2つの変数間の線形関係の強さと方向を数値で示します。
2つの変数間というのは、例えば次のような関係性です。
- 親の身長と子の身長
- 売上金額と来店客数
- 滞在時間と顧客単価
- 間取りの数と家賃
- etc…
相関係数を求めるためには、どちらも「量的変数」でなければいけません。「量的変数」というのは、四則演算ができる種類のデータである、ということです。
相関係数は-1から+1の間の値を取り、0~1 までの範囲を正の相関、-1~0 までの範囲を負の相関と表します。
0に近しい係数の場合、変数間に相関は認められないと判断します。それでは、正の相関と負の相関について見ていきましょう。
正の相関
正の相関とは、片方の変数が増えると、もう片方の変数が増える関係性です。
- 気温が上がれば、ビールの売り上げが伸びる
- 来店客数が増えれば、売上金額が上がる
- クリック数が増えれば、商品の注文数が上がる
このような関係性です。
負の相関
負の相関とは、片方の変数が増えると、もう片方の変数が減少する関係性です。
- 気温が下がれば、ダウンジャケットの売り上げが伸びる
- 訓練時間が増えれば触れるほど、作業時間が減る
- 広告の表示頻度が多ければ多いほど、クリック数が減少する
用語で「負」という文字を使うので、ネガティブなイメージがついてしまうかもしれませんが、決して負の相関だからダメ、ということはありません。
相関係数の求め方
ExcelのCORREL(コリレーション)関数を使えば簡単に求まりますが、この記事では計算フローを箇条書きでご説明いたします。
ここでは、お店の「滞在時間」と「売上」の2変数について考えてみましょう。
- 滞在時間と売上、それぞれの平均値を出力する
- 各滞在時間と各売上の偏差(平均からの差)を求めていく
- 各滞在時間と各売上の偏差を1組ずつ乗算する
- ③の合計値を件数で除算する。この値を共分散という
- 滞在時間と売上の標準偏差(母集団として)を出力する
- 共分散÷2つの標準偏差の乗算で、相関係数が求められる
2つの標準偏差を掛け合わせた値を分母として共分散を割るため、必ず-1~1の間にデータが収束します。不思議な数の性質ですよね。
以下、データ件数100件、とあるコンビニエンスストアの滞在時間と顧客単価を表示したデータです。
計算フローが長いのですが、①~⑥までを凝縮したExcelの計算例を画像で添付しておきます。じっくり読み解いてみてください。
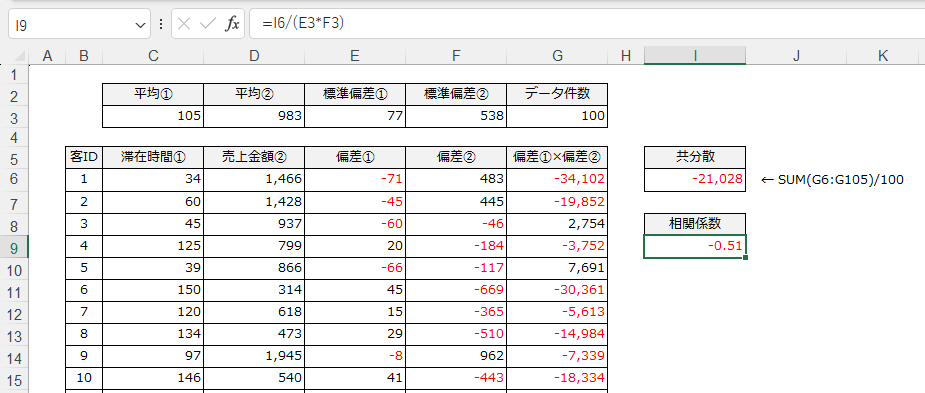
相関係数は「‐0.51」と算出されました。この読み方については次に説明をします。
相関係数の度合い
以下の表のとおりです。
| 相関係数 | 相関の度合い |
| -1.0 ~ -0.7 | 強い負の相関 |
| -0.7 ~ -0.4 | やや強い負の相関 |
| -0.4 ~ -0.2 | 弱い負の相関 |
| 0付近 | 相関なし |
| 0.2 ~ 0.4 | 弱い正の相関 |
| 0.4 ~ 0.7 | やや強い正の相関 |
| 0.7 ~ 1.0 | 強い正の相関 |
先ほどのサンプルデータの相関係数は「-0.51」なので、やや強い負の相関の部類に入ります。つまり、店舗の滞在時間が短ければ、客単価が高くなる傾向にある、と読み取ることができます。
サンプルデータなのでここまでの結論ですが、実際は総合的に判断して、最適な顧客の滞在時間はどこか? を分析していきます。そこをひとつの目標として、店舗のレイアウトを見直し、実験に映っていくといった流れをたどっていきます。
それでは、相関係数から始まる分析の流れを見ていきましょう。
相関関係からの一般的な分析の流れ
顧客の滞在時間と顧客単価には関連性があるだろうか? もしあるのであれば、少しでも顧客単価を上げるために、店舗のレイアウトなどを見直したい。
最適な滞在時間を設定して、そこに平均滞在時間が近づくようにレイアウト変更し、実験をしてみる。そして、実験前と実験後で顧客単価がどう変わったかを比べてみる
別の店舗でも同じような結果になるか? 再現性の確認をしてみる
再現性が取れれば、この分析は成功となります。顧客単価は顧客の滞在時間と関係性があるといえる判断をして、マニュアル等更新、全店舗に反映します。
ただし、永続的にこれが通用するものではないことを認識しておくことが必要です。時代によって顧客の購買行動・購買心理は変化していくものですからね。
相関係数の読み方
相関係数と相関の度合い、そして分析の流れについては以上のとおりですが、先ほどの事案を1としましょう。
別の事案2でも、同様の相関係数が「‐0.51」が計算されたとします。果たして、この2つの相関係数は、同じ相関の度合いだといえるでしょうか?
答えは、同じ相関だとは言えません。
事案1と事案2は、たまたま同じ相関係数が算出されただけであって、まったくの別物です。相関係数は、その2変数の関係性だけで見るようにしてください。
また、この一覧表は教科書的なものです。特に、金融の世界では「-0.2」程度の値が出れば、買いに出たり、売りに出たりします。業種によって扱いも全く異なるんですね。
例えば、三井住友信託銀行が窓口となっている投資信託では、ゴールド・ファンドとJリートのファンドがあります。
これらは、金と不動産に関するファンドです。
2つのファンドはおおよそ負の相関係数にあるため(世の中が安定すると金の価値が下がり、世の中が不安定になると金の価値が上がるとされています)、負の相関があるファンドに投資をしておくと、片方がいいときに片方が悪い状態で資産運用ができるため、ローリスクな資産運用の典型的事例です。
私自身もこのような買い方で投資信託の商品を購入していますが、といっても400万円の資産運用で、年間20万円ぐらいの利益が限度でしょうか。
ローリスクな買い方は、ローリスクなリターンです。
源泉徴収税額で結局持っていかれるので、そんなには儲かりませんが、それでもまあ銀行で寝かせているよりかは、いい資産運用を継続しています。
相関係数は、このような判断材料としても使うことができるので面白いですよね。長くなりましたが、相関についてのお話は以上となります。
統計基礎ブログはひとまずここまでです。また随時追加していく予定ですが、いったんはおつかれさまでした。



