期待値とは？　カイ2乗検定を学習する前に

この「期待値」も、学習のハードルが高いキーワードです。まず、教科書的な説明から入っていきましょう。

期待値とは、ある事象が繰り返し発生した場合において、「平均して」どれくらい起きるかを示した数値です。

日々の生活の中でよく使う「平均」という概念が似ておりますが、期待値は特にチャンスやリスクが絡む状況で、その結果を予測するために使われます。

この数値は、ゲームでの勝ち負けの予想から、ビジネスの収益予測、さらには科学実験の結果分析に至るまで、さまざまな場面で役立てられます。

日常的に直面する不確実性を理解しやすくするのに役立つ値です。

期待値の事例 ①　サイコロ

例えば、サイコロを６回振って、出た目の数をポイントとしましょう。

それぞれ１～６の目が１回ずつ出ることが平均的と言えるので、１～６を足した「２１」を「６」で割った「3.5」の値が期待値となります。

つまり、サイコロを繰り返し振り続けた場合、１回あたりの得点が「3.5」ポイントになることを表しているのです。

期待値の事例 ②　商店街の抽選くじ

サイコロの説明はありきたりなので、もう１例、商店街の抽選くじを考えてみましょう。

売上予算を100万円に設定、その20%（20万円）を還元祭としたケースを想定します。1,000円のお支払いにつき、1枚の抽選くじを渡す、というルールにしましょう。

1,000円の20％、景品に割り振る期待値「200円」となるくじの設計を目指していきます。つまり、1回の抽選で200円が支払われている、と考えることができます。

景品の割り振り計画

• 売上予算： 100万円
• くじの販売数： 100万円 / 1,000円 = 1,000枚
• 景品予算： 20万円

景品の割り振り

期待値を200円に設定するために、1,000枚のくじに対して、合計で20万円分の景品を用意します。

ここでは、具体的な割り振りを提案し、各等級の景品に割り当てる予算と、当選確率を計算してみましょう。

景品の価値設定と当選確率：

• １等：3万円分の商品 x 1本
• ２等：1万円分の商品 x 3本
• ３等：5,000円分の商品 x 10本
• ４等：1,000円分の商品 x 50本
• ５等：100円分の商品 x 余剰分（当選確率を調整して期待値を合わせる）
• 参加賞：５等の余剰分

この内訳は、ざっくばらんで決めています。

抽選くじに来てもらえるような配分を目指していきましょう。１等から４等までの景品にかかる予算を計算し、残った予算を５等にどのように割り振るかを考えます。

• １等：3万円分の商品 x 1本（当選確率 0.1%）
• ２等：1万円分の商品 x 3本（当選確率 0.3%）
• ３等：5,000円分の商品 x 10本（当選確率 1%）
• ４等：1,000円分の商品 x 50本（当選確率 5%）

ここまでの使用金額は、16万円。

残り3万2000円を５等の景品に、8000円分を参加賞にすべて割り当てます。

• ５等：100円分の商品 x 320本（当選確率 32%）
• 参加賞：５等の余剰分 x 616本（残額8,000円で参加賞作成）

8,000円もあれば、ポケットティッシュを人数分オーダーできるでしょう。

これらの設定により、期待値はちょうど200円になり、５等の当選確率が32%に設定されました。当選確率を見せてしまうと、ほとんどがポケットティッシュになりうるくじ引きでもありますが、くじ数も1,000で構成されていい感じに収まりました。

冒頭にも説明した、ある事象が繰り返し発生した場合において、「平均して」どれくらい起きるかを示した数値は、このように使うこともできるわけです。

カイ2乗検定での期待値

続いて、カイ2乗検定で登場する期待値の計算です。

ABテストをするにおいて、どちらのほうがパフォーマンスがいいのかを測定することができるか、カイ2乗検定をする前の途中計算で期待値を求めます。

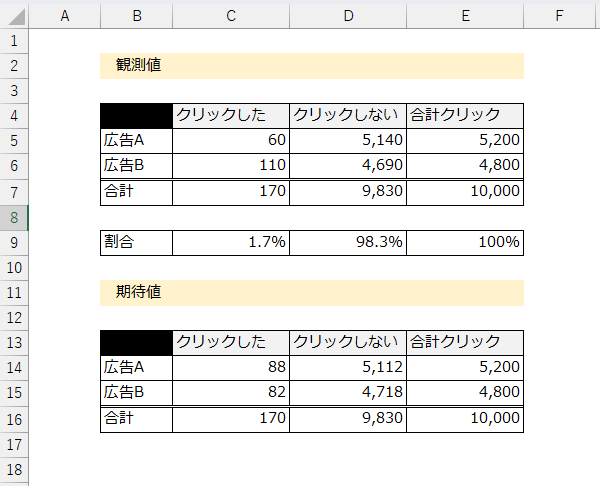
この期待値が？な方がとても多いので、先ほどの商店街の例と紐づけてみてください。

広告Aは合計クリック「5,200」ずっとされるのであれば、クリックした期待値とクリックしていない期待値はキャプチャのとおりになります。

また、広告Bの合計クリックが「4,800回」ずっとされるのであれば、クリックした期待値とクリックしていない期待値はキャプチャのとおりです。

広告Aはどうして観測値では「60」なのに期待値だと「88」なの？　というご質問が多いのですが、クリック数が5,200、広告Bよりも多いからです。

カイ2乗検定では、観測値と実測値の２つを使って、この２つに意味のある差は発生しているか否かを計算で求めていきます。以上が、期待値の説明でした。

まとめ

いかがでしたでしょうか？　カイ２乗検定は「質的変数」と「質的変数」の同士の分析、そもそも情報量が少ない検定なので、かなり難しいです。

その難しさを誘発させているのが、この期待値。この期待値をしっかりと把握することができれば、カイ２乗検定は怖くありません。それでは、続いてカイ２乗検定のブログに進んでいきましょう！

こちらの記事は以上となります。おつかれさまでした。

榊 裕次郎

Excel講師

1981年10月生まれのてんびん座、東京都出身。趣味は、旅行と料理とワイン。2024年は、佐賀県に行って「呼子のイカ」を思いっきり食べたいです。

引き続き、青森・秋田・岩手でのお仕事ご依頼、お待ちしております！