度数分布表について

度数分布表は、統計学の基本的なツールです。データがどのように分布しているのかをまとめ、それをヒストグラムというグラフで可視化します。

統計の多くのテキストでは、度数分布表がすでに作成されていることが多く、ゼロから作成する演習はあまりありません。

この記事では、ゼロから作成する方法もご紹介してまいります。

度数分布表では、用語がこのように多いセクションです。階級の設定方法を覚えておくと、とても便利ですよ

第14講座

度数分布表には、以下の要素が含まれます。

度数分布表の用語

階級（ビン）

階級とは、データを分類するための範囲のことです。年齢区分がわかりやすいでしょう。

• 10歳未満
• 10歳～20歳未満
• 20歳～30歳未満
• 30歳～40歳未満
• 40歳～50歳未満
• 50歳～60歳未満
• 60歳以上

このように区切りよくグループ化し、データを振り分けます。階級は、なるべくわかりやすい区分で作成する必要があります。

加えて、「60歳以上」という区分のように、データ件数が少ないと明らかに想定される場合、100歳区分まで同じ間隔を継続して区切る必要はなく、このようにまとめることも大切です。

また、階級を英語で（bin）と呼び、このように区間分けすることをビン化するという表現を使います。これは資格試験などによく出てくる用語ですね。

度数

各階級に含まれる、データの件数のことを言います。

相対度数

全データに対する、各階級の度数の割合です。

例えば、調査人数が「100」人で、20歳～30歳未満の度数が「20」人だとしたら、相対度数は「20％」となります。

累積度数

ある階級までの度数の累計です。

こちらも全体が「100」人として、10歳未満が「5」人、10歳～20歳未満まで「15」人、20歳～30歳未満まで「20」人としましょう。

30歳未満までの累積度数は、累積で「40」人と計算されます。

累積相対度数

ある階級までの相対度数の累計です。④ 累積度数の例でいうと、30歳未満までの累積相対度数は100人のうちの40人ということで、「40％」となります。

以上が、度数分布表の用語です。

ビン化する、という用語は階級にまとめるという意味があります。連続したデータをまとめることで、各レンジごとにグルーピングして分析することができます！

階級数の決定方法

階級数とは、階級の数のことを指します。先の例で、

• 10歳未満
• 10歳～20歳未満
• 20歳～30歳未満
• 30歳～40歳未満
• 40歳～50歳未満
• 50歳～60歳未満
• 60歳以上

と、区切った場合の階級数は「７」となります。

一般的に階級数は自由に設定して問題ありません。年齢の場合は、特に問題なく10歳ずつの階級分けが想定できますが、売上金額の階級分けや、店舗滞在時間の階級分けなどを考えた場合、どこを区切りとするのかが悩むところです。

売上の場合は顧客単価によって変動しますし、店舗滞在時間は店舗の広さ、店舗のジャンルなどによっても変わります。

ここで、階級数の目安を算出する２つの計算式をご紹介します。

階級数の最適な設計の仕方

階級数の求め方は、以下の２点です。

データ件数の平方根法

データの総数の平方根を階級数の目安とします。

例えば、データ件数が100件の場合、階級数の目安は √100 ＝ 10 となります。つまり、階級数が10区間前後あればいい、という目安を設けることができます。

あくまで目安です。10階級に絶対分けなければいけない、というわけではありません。

スタージェスの公式

統計学者のハーバート・スタージェスさんが1926年に考案した公式です。

彼は、1+3.322log₁₀​N という公式を提唱しました。

N に入る値は、データの件数となります。

公式は難解なのですが、データ件数が「100」の場合、シンプルに log₁₀​N の部分が「2」（10の2乗は100。対数の計算です）になるので、

1＋3.322×2 = 7.644 となります。

別解として、1+log₂N でも似た値を求められます。

こちらは暗算ではできないので、同じようにデータ件数「100」の場合で、ExcelのLOG関数を使って計算してみましょう。

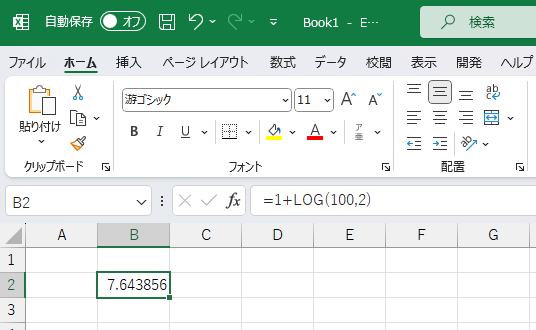
答えは四捨五入して「7.644」となります（この一致は偶然で、データ件数に応じて多少の誤差は出てきます）。

ですので、スタージェスの公式で求めた場合と、スタージェスの公式に似た別解の値で求めた値、どちらも目安となる階級数は切り捨てて「7」となるわけです。

以上が、階級数の目安を探る手法でした。

この２つの手法で階級数の目安を求め、7～10の階級数であればちょうどいいだろう、と判断できるでしょう。

ただし、繰り返しになりますが、階級数はわかりやすさが命です。無理に階級を目安に合わせて、わかりにくい度数分布表になるのであれば、それは間違いです。

わかりやすさを正義としてください。

度数分布表の作成手順

最後に、度数分布表の作成手順です。おそらくExcelを使って度数分布表を作成することがほとんどかと思いますが、ここでは手順だけを記載しておきます。

データの範囲を決定

最小値と最大値を確認して、レンジ（データ範囲）を把握します。

階級数を決定

データの平方根法またはスタージェスの公式を用いて、階級数を決定します。

階級幅を決定

①と②参考にしながら、わかりやすい階級幅を割り出します。それにより、階級数を調整します。今回は階級数「７」がわかりやすいので、７つの階級を採用したとします。

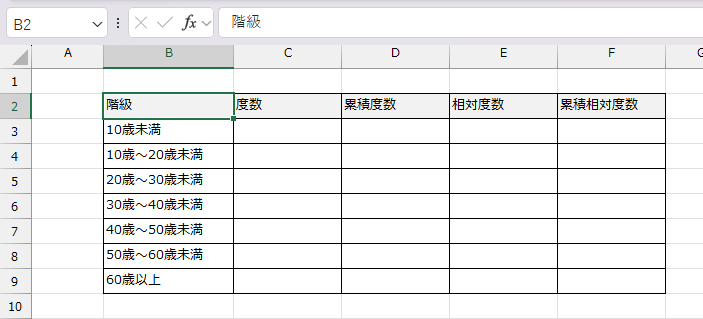
各階級の度数を数える

各階級にデータがいくつあるかを数えます。Excelの場合では、FREQUENCY（フリークエンシー）関数や、データ分析ツールのヒストグラム機能、またはCOUNTIFS関数を使って求めることが可能です（この操作説明は割愛します）。

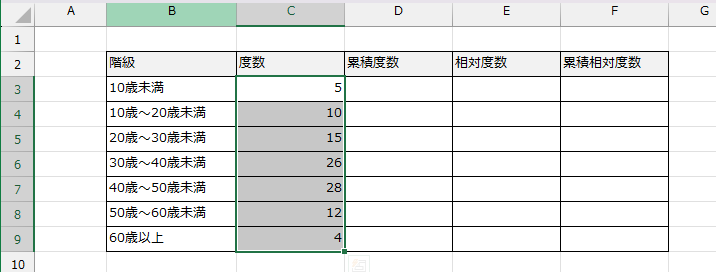
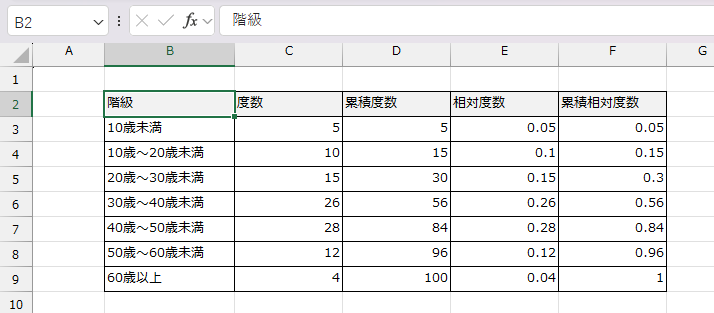
相対度数と累積度数、累積相対度数を計算

全データに対する各階級の割合を計算し、そこから相対度数、累積度数、累積相対度数を求めて完成です。以下のキャプチャが完成サンプルです。

度数分布表の有用性

このように、度数分布表を使ってデータを階級分けすることで、データの分布パターン、中心傾向、ばらつきの程度をまとめることができます。

例えば、タクシー会社が保有する車両の走行距離を分析するケースを考えてみましょう。

度数分布表を用いると、どの車両が多く走行しているのか、または少なく走行しているのかを一目で確認することができます。

これにより、車両のメンテナンススケジュールの計画や、新しい車両の購入計画に役立つ情報を取得することができるでしょう。

次の記事では、この度数分布表を使った「ヒストグラム」というグラフついてご紹介いたします。まずは、度数分布表で必要となるキーワードを押さえておきましょう。

次にご紹介する度数分布表からのグラフを、ヒストグラ「フ」と読み方は間違えないようにしてください。ヒストグラ「ム」です。

榊 裕次郎

Excel講師

1981年10月生まれのてんびん座、東京都出身。趣味は、旅行と料理とワイン。2024年は、佐賀県に行って「呼子のイカ」を思いっきり食べたいです。

引き続き、青森・秋田・岩手でのお仕事ご依頼、お待ちしております！