調和平均について

恥ずかしながら、私が学生時代に全く理解できなかったのが「調和平均」です。

中学の数学で先に学び、そのあと理科のオームの法則で合成抵抗が出てくるので、そこでも習った内容だと思います。

ここまでで、相加平均、相乗平均と学習しました。こちらの記事では「調和平均」を学習していきましょう。

逆数の平均の逆数だって言われても、さっぱりだったよ

調和平均

調和平均は、逆数の平均の逆数を取ることで計算されます。

例として「60」と「100」の値で、相加平均では「80」になりますが、調和平均では「75」と算出されます。これが本当に理解できませんでしたw

以下、それぞれの計算式を記載いたします。

どうして、逆数の平均の逆数なんて面倒くさいことをするのか？　この計算式が当時まったくわかりませんでした。

しかし、大人になって機械学習を学び、ようやく理解に及びました。長かったね。

調和平均の理解の仕方

60と100の2つの数字を強弱で考えると、100のほうが強いですよね。では、これを逆数にするとどうなるでしょうか？

1/60 と 1/100 になります。こうすると、1/60 のほうが強くなりますよね？

逆数にすると、小さな値は大きな値になり、大きな値は小さな値になります。この強・弱を入れ替えて平均を求めるのが「調和平均」の本質です。

調和平均の使いどころとして、

• 速度（距離 ÷ 時間）
• 生産効率（作業量 ÷ 時間）
• 電気抵抗（電圧 ÷ 電流）

など、「分母が変化する指標」を扱うときに本領を発揮します。

往路・復路の自動車移動の例を出してみましょう。

10キロメートルの道路を、往路は時速60キロメートル、復路は時速100キロメートルで走った場合の平均時速は、調和平均により75キロメートル/時と計算されます。

分母が変化する、という意味を考えてみましょう。つまり、

• 速いほう（100km/h）は、短い時間しか走っていない
• 遅いほう（60km/h）は、長い時間を占めている

平均速度を求める際、行きと帰りで分母に変化がありますよね。こういうケースのとき、遅いほうに引っ張られるのが正しい平均となります。

どうでしょう？

2往復目にこの10キロメートルを平均80キロで走らなければいけない！　というのと、平均から5キロ減の75キロで十分だよ！　というのでは、後者のほうが安全に聞こえますよね。

合成抵抗も同じ理由になります。調和平均のほうが弱い抵抗に力を合わせてくれる。小さな数字を優しく扱う平均値。これが調和平均なのです。

このように考えると、調和平均の使いどころがわかりやすくなりませんか？

Excelでの調和平均を求める関数

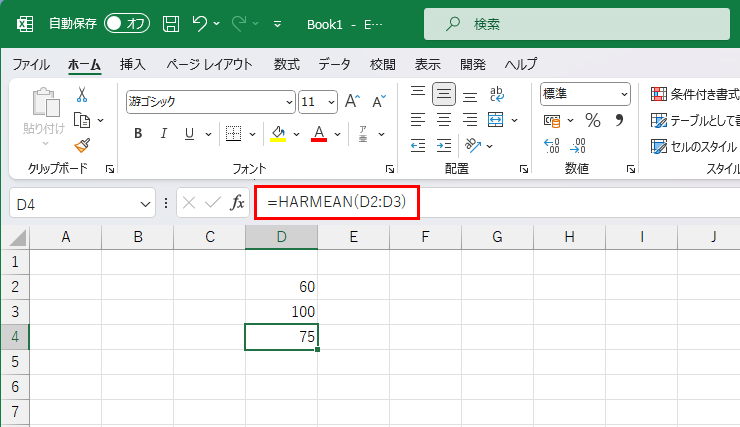
Excelでは、HARMEAN（ハーミーン）関数を使います。使い方はAVERAGE関数と同様なので、上のキャプチャのように計算してみてくださいね。

まとめ

特定の条件では、強い数字を弱い数字に変換して平均を取る。これが調和平均でした。

補正の入った調和平均は、相加平均よりもマイナスの値で出力されます。統計学では調和平均を使うシーンはあまりないのですが、機械学習ではよく用いられますね。

以上、調和平均でした。

上流と下流で力関係を逆数を使って入れ替える、ってところが斬新な計算式だなと感じました！

最終確認日：2025年11月22日

榊 裕次郎

Excel講師

1981年10月生まれのてんびん座、東京都出身。趣味は、旅行と料理とワイン。2025年もラストスパートですね！　皆さんはどんな１年でしたでしょうか？

2025年が最後までいい１年でありますように、がんばっていきましょう！