ヒストグラムについて

度数分布表を可視化するための縦棒グラフをヒストグラムと言います。ヒストグラフと読み間違えないように注意してくださいね。

ヒストグラムは、度数分布表の情報を可視化するのに役立ちます。この記事では、ヒストグラムの作成方法と、グラフの読み方について解説していきます。

ここでのポイントは尖度と歪度。正規分布の波形をイメージしながらデータの全体像を推測していきましょう！

第15講座

ヒストグラムは、エクセル講師らしくExcelを使った操作の流れでご紹介しましょう。まず、度数分布表を完成したところからスタートしていきます。

最初に、完成した度数分布表の「階級」と「度数」を範囲選択します。

[挿入]タブから、2-D 縦棒を選択していきます。

初期設定の棒グラフが作成できました。

グラフの書式設定で、この縦棒グラフ同士の余白間隔を詰めていきます。どの縦棒でも構わないので、右クリック → [データ系列の書式設定] をクリックします。

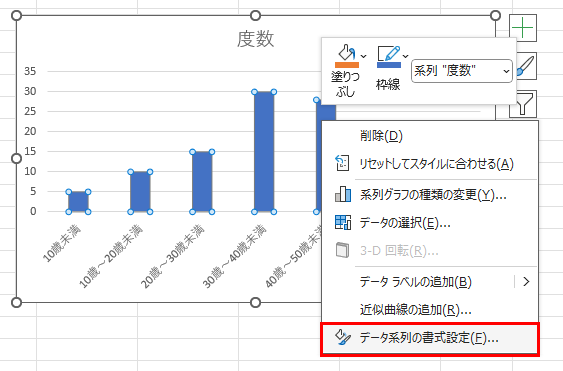
画面右側に書式設定ツールが出てきました。初期値では「219％」になっています。

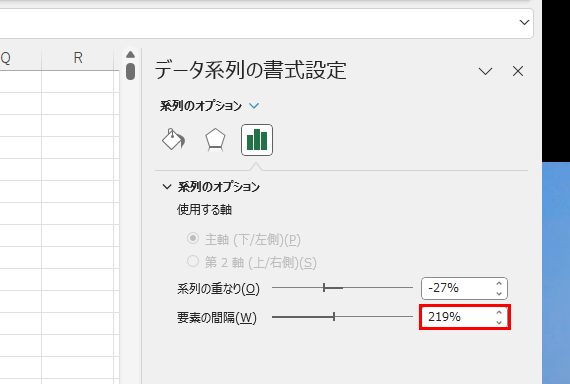
この値は、棒グラフの幅を１としたとき、次の棒グラフの余白まで2.19倍の間隔をあけますよ、という意味になっています。

これを「0％」にしてしまいましょう。

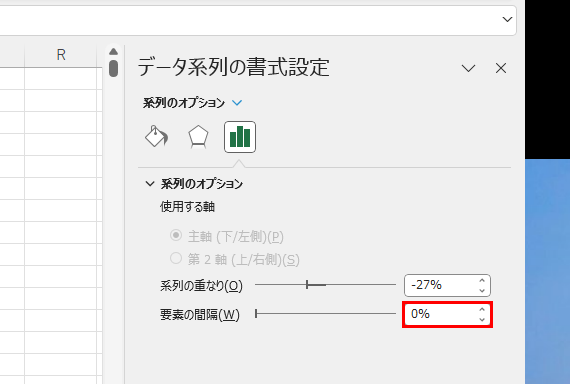
こうすることで、棒グラフの間隔が詰められ、ヒストグラムが完成しました。

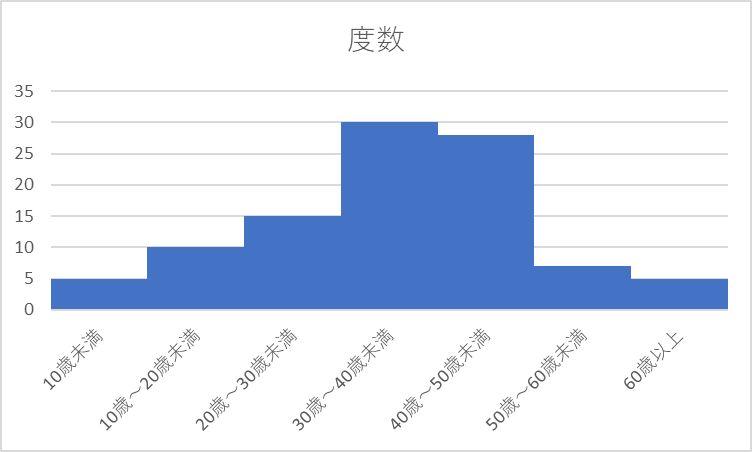
あとは書式設定を整えて完成です。

さて、このヒストグラム。見た感じでは、正規分布に近い、全体的にはバランスのいい分布でもありそうです。

それではここで、基本統計量に含まれる代表値、⑨ 尖度 と ⑩ 歪度 について学習をしていきましょう。この値があることで、より正確にヒストグラムの状態を読むことができます。

⑨ 尖度と ⑩ 歪度

基本統計量にもある「尖度」と「歪度」という値を学習していきます。

尖度（せんど）の読み方は問題ないかと思いますが、歪度（わいど）は独学での初見では読めませんでした。

それぞれ、「とがり」と「ゆがみ」のことを指しています。

基準は正規分布で、尖度と歪度が０の値であれば、正規分布の釣鐘状をしたバランスのいい形であることが想定されます。

尖度の値の読み取り方

尖度が０より大きい場合は、データが正規分布に比べて尖っていることを意味しています。尖っている＝データがどこかの階級に集中している、とも読み取れますね。

逆に、尖度が０よりも小さい場合は、正規分布よりもだらっとした偏平形状の分布になっており、ばらつきが大きく、データが点在していることが伺えます。

以下、イメージ図です。

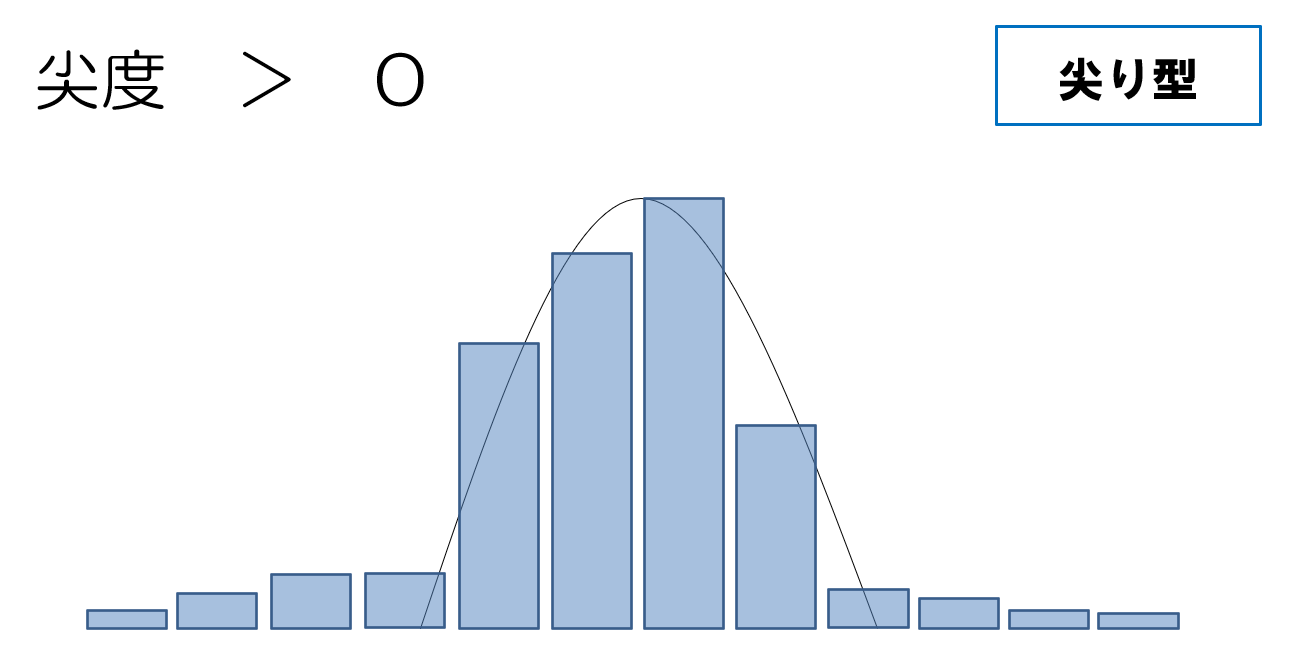
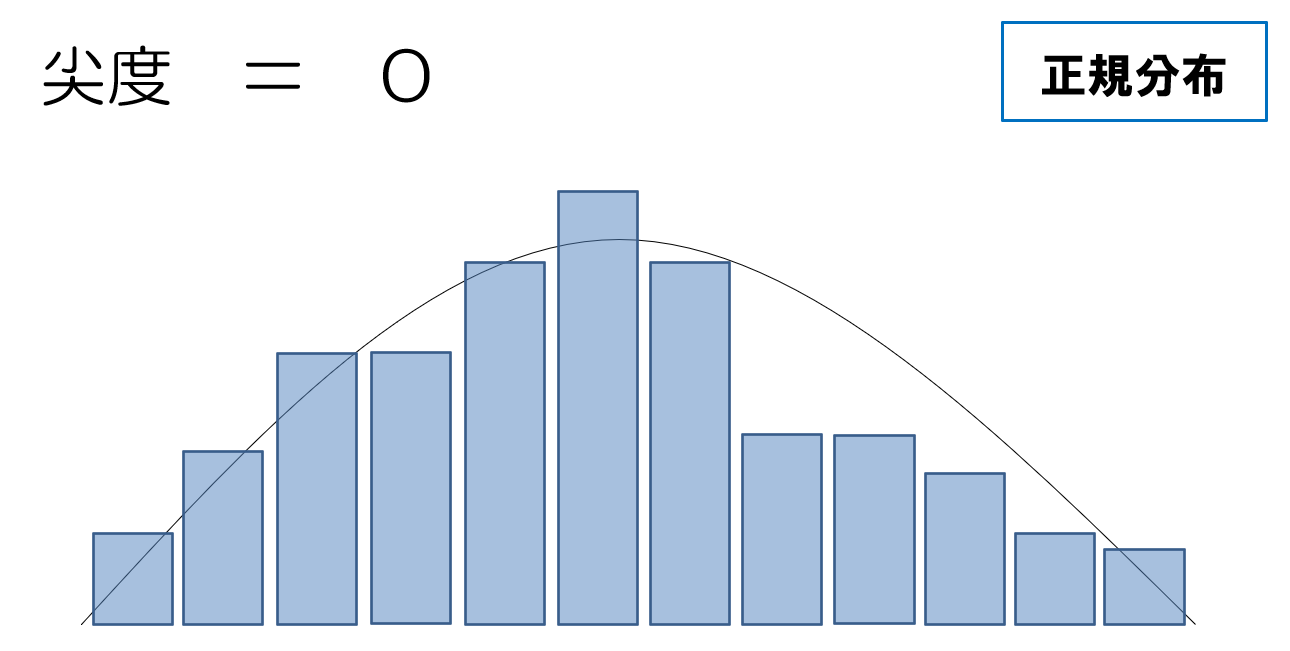
こちらはイメージがしやすいでしょう。

歪度の値の読み方

正規分布の釣鐘状をした形を、プリンだと思ってください。

歪度が０より大きい場合は、左にぷるんと動いたような波形になります。その逆に、歪度が０より小さい場合は、右にぷるんと動いたような波形になります。

歪度 ＞ 0 で左側。歪度 ＜ 0 で右側。不等号の記号で覚えるようにしてください。

同じようにイメージ図を用意しました。

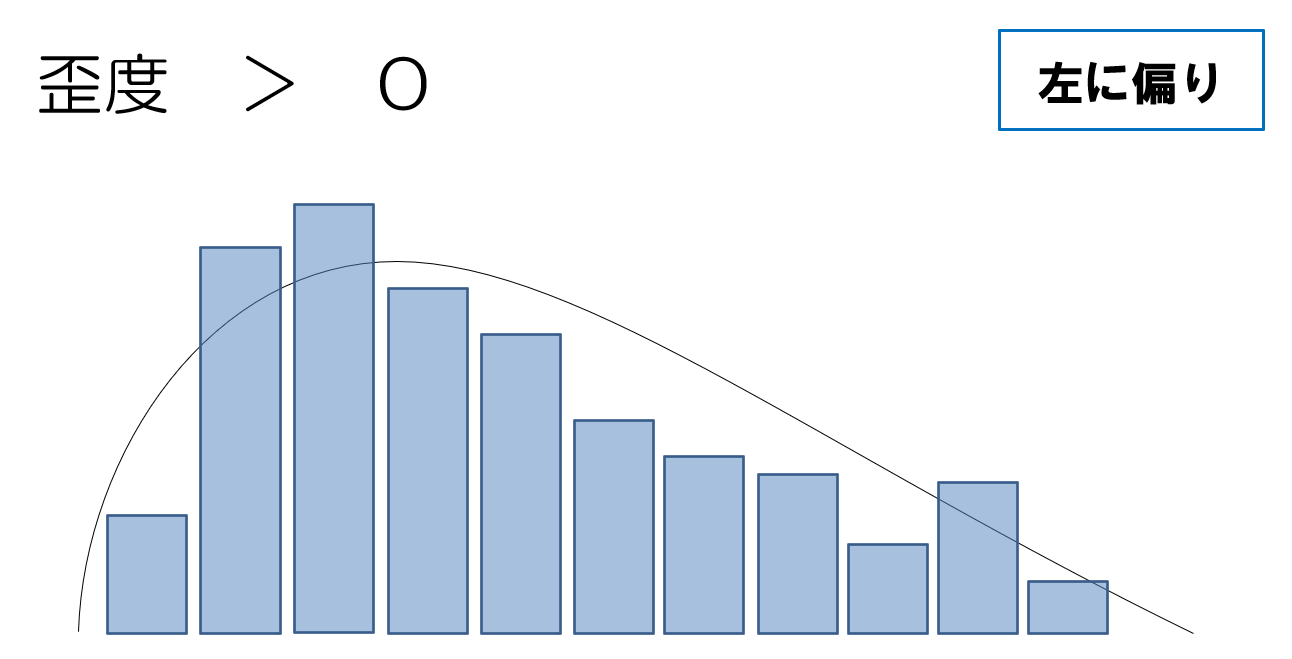
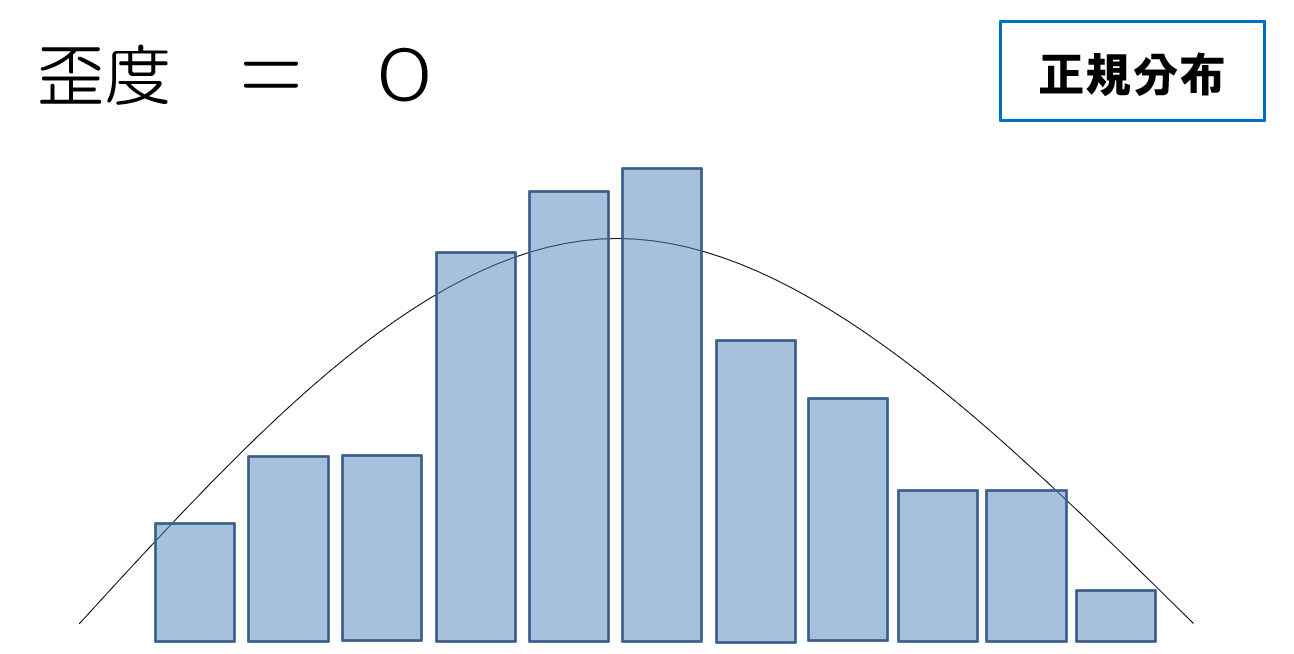
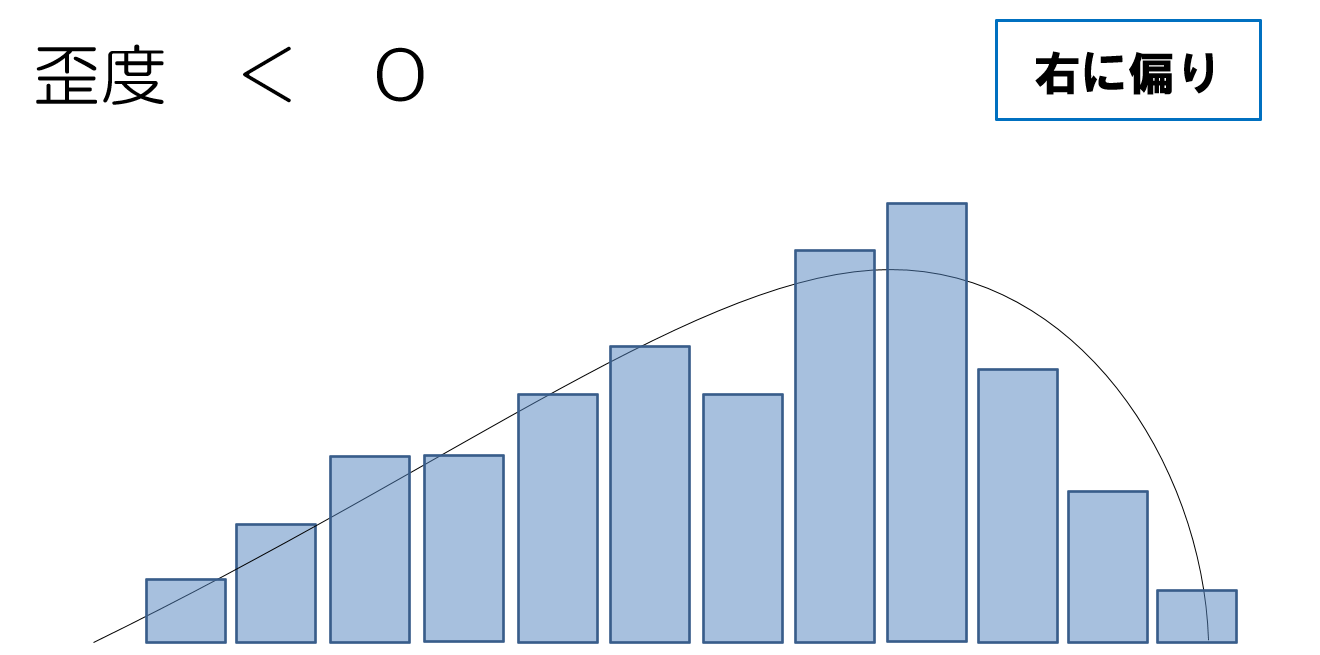
では、今回のヒストグラムはどのような値か見ていきましょう。

ダミーデータのため少し精度は悪そうですが、以下のような値になりました。

• 尖度：-0.61
• 歪度：0.05

正規分布図よりも若干偏平ではあるものの、左右の偏りも平均的で、バランスのいいヒストグラムであると読み取れます。

もうひとつのダミーデータで、尖度と歪度を見てみましょう。

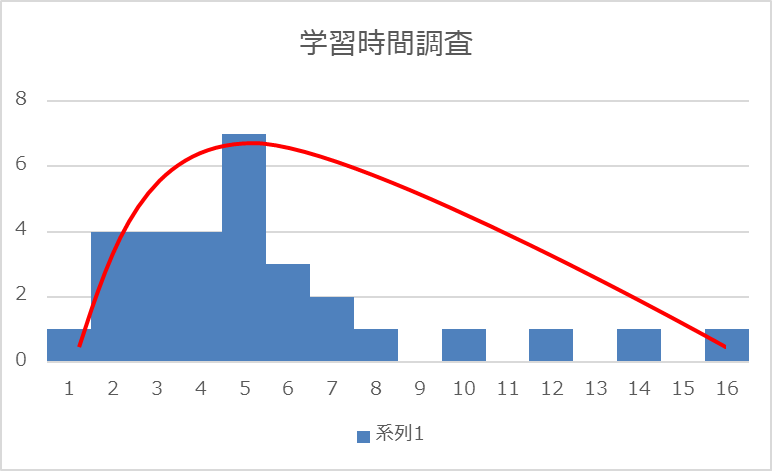
• 尖度：2.41
• 歪度：1.55

イメージとして赤の補助線を引いてみました。正規分布よりも尖っており（どこかにデータが集中している）、左に偏った波形であることが想定されます。

尖度と歪度では、ここまでしか情報量としては引き出せませんが、ヒストグラムを見ただけでは、個人の感想にしかすぎません。しかし、この２つの値を見ることで、どちらに偏りがある・なしを数字的な裏付けをもって説明することができます。

この尖度と歪度を出力する方法は、Excelではデータ分析ツールを使ったり、KURT（カート）関数とSKUE（スキュー）関数で尖度と歪度を求めることができるのですが、算出方法に関しては、別の記事で改めてご紹介したいと思います。

この記事では、尖度と歪度の値でどのような波形になっているのかを覚えておきましょう。

ヒストグラムの読み方

ヒストグラムの山の形は、５パターンほどあります。

一山型

正規分布のようにバランスの取れた分布図です。

二山型

異なる２種類の属性が混じっているパターンです。

例えば、テストの得点で40点のグループと70点のグループに山が分かれていた場合、クラスの学習習熟度は二極化してしまっている、ということがわかります。

データパターンとしては、問題点が浮上するヒストグラムですね。

離れ小島型

外れ値がデータ群の中に含まれている場合、離れた階級にぽつんと度数が出現するため、離れ小島型と呼ばれています。

その小島が外れ値、異常値、計測エラー値などであることを確認する必要があります。

歯抜け型

度数がバラバラになっていて、バランスが取れていないヒストグラムを歯抜け型と呼びます。これは階級の設定に問題があることが多いです。

階級を見直すところからやり直す必要があります。

裾引き型

これは１つしかありません。貯蓄現在高等級のようなグラフです。ずっと尾を引くようなヒストグラムのことを指します。

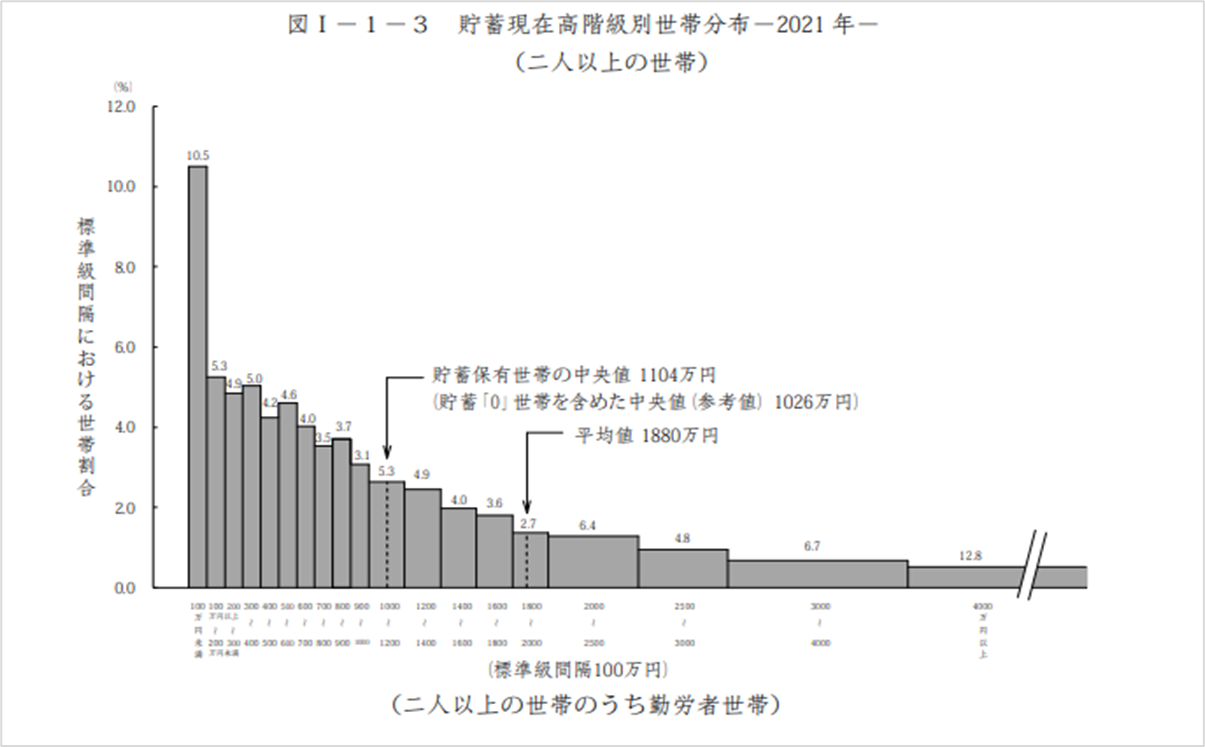
ヒストグラムの波形は以上です。データの全体像を把握するツール、それがヒストグラムでした。

平均値・中央値・最頻値も貯蓄現在高等級のヒストグラムを見ながらどういう順番になるのかもイメージしてみてね

榊 裕次郎

Excel講師

1981年10月生まれのてんびん座、東京都出身。趣味は、旅行と料理とワイン。2024年は、佐賀県に行って「呼子のイカ」を思いっきり食べたいです。

引き続き、青森・秋田・岩手でのお仕事ご依頼、お待ちしております！