MEDIAN(メジアン)関数の使い方
MEDIAN(メジアン)関数は、セルに含まれている各数値データの中央値または中間値を求めてくれる関数です。
【構文】
=MEDIAN(数値1, 数値2……)
【使用例】
- =MEDIAN(B2:B6)
セルB2~B6までの数値データの中央値を出力します。 - =MEDIAN(Sheet2!B2:B5)
別シート「Sheet2」のセルB2~B5までの数値データの中間値を算出します。
[char no=”1″ char=”さえちゃん1”]中央値を割り出す際、計算対象となるデータ数は必ず奇数でなければなりません。データ件数が偶数の場合、真ん中の数を取ることができませんからね。件数が10の場合、昇順に並び替えをして、5つ目と6つ目の間のデータを算術平均で求めた数、中間値が中央値の代わりとなります。中央値と中間値は別の値なので、混合しないよう注意してくださいね。[/char]
関数説明
MEDIAN関数は、データ件数が奇数の場合は「中央値」を求め、データ件数が偶数の場合は「中間値」を求める関数です。
まずはデータ件数が奇数の場合の動きを見てみましょう。
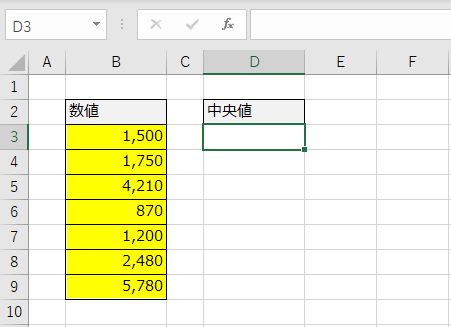
MEDIAN関数は、[数式]タブ→[その他の関数]→[統計]の中にあります。
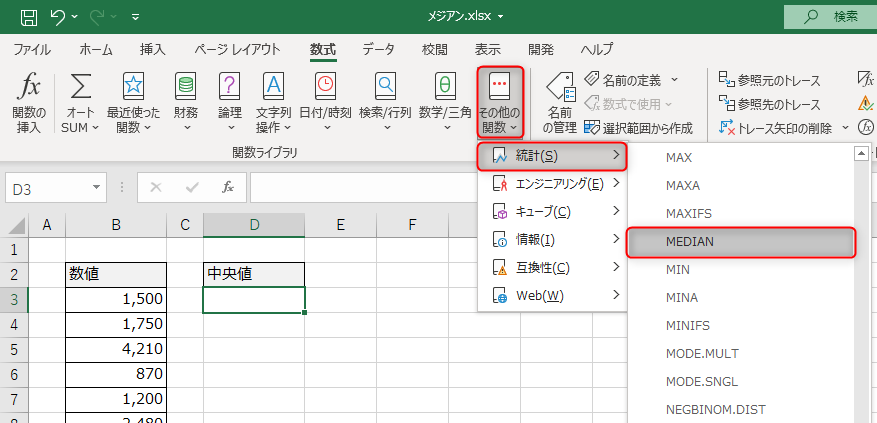
使い方はSUM関数と一緒です。
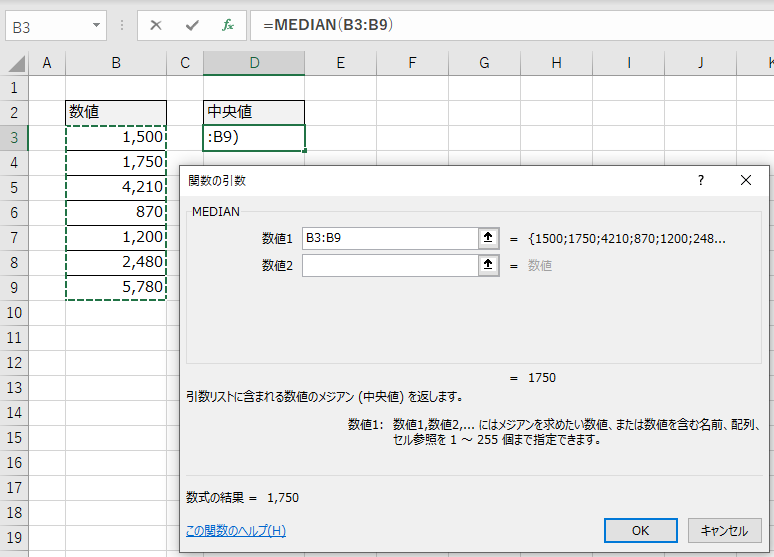
離れたところの数値を取得したい場合は、数値2以降を使います。今回はセルB3~B9までの間なので、数値1で範囲選択ができました。
OKボタンをクリックします。
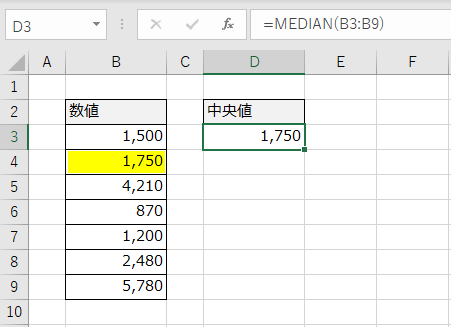
7つのデータの真ん中の値「1,750」が取得されました。
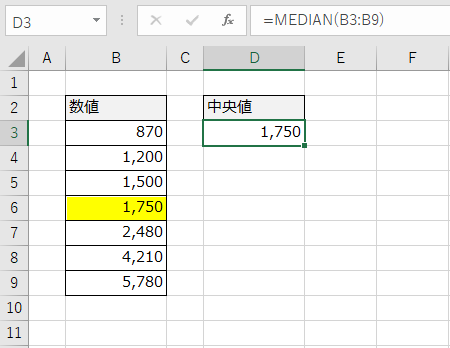
念のため、昇順に直してみましょう。
きちんと真ん中の数値データでした。続いて、データ件数が偶数の場合を求めてみます。
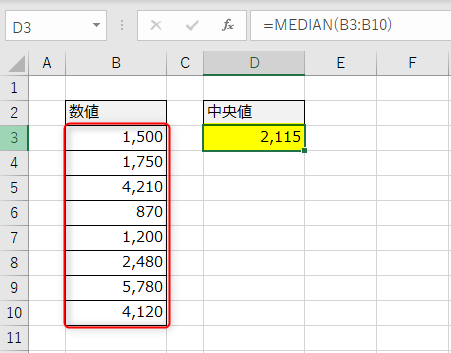
答えは「2,115」となり、中間値が出力されました。
中間値は、以下の昇順に並び替えをした黄色いセルのように、間の上下二つのデータをAVERAGE関数で算術平均した値と同じになります。
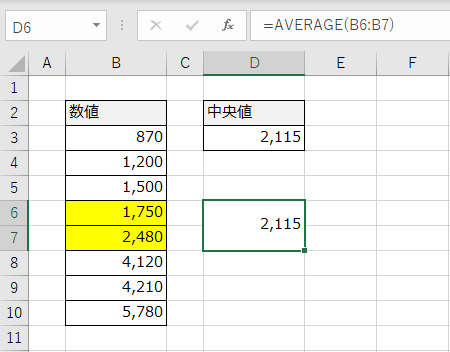
存在していないデータが出力されるため、存在しているデータである中央値とは異なります。そのため、中央値を出すときはデータの件数が奇数でなければなりません。
ただし、データを分析する際には、中央値も中間値も外れ値の影響を受けていない代表値のひとつなので、中央値だから、中間値だから、というだけで分析結果が大きく変わるものでもありません。
中央値も中間値も、これがこのデータの中でちょうど真ん中の値、として活用してください。
さえちゃんのMEDIAN関数ワンポイントアドバイス
[char no=”4″ char=”さえちゃん3”]データを見るとき、MEDIAN関数を使う前に、必ずAVERAGE関数で平均を算出します。一般的にデータの代表値を探すときは、まずはAVERAGE関数です。ただ、AVERAGE関数の値では、酒豪下戸が集まる飲み会のように、誰かががぶがぶ飲んでバクバク食べてしまったら、お会計は高い金額に引っ張られてしまう性質があります。中央値を見ることで、そのデータがどちらに傾いているのか? を簡単に把握することができるんですね。[/char]
AVERAGE関数のサンプルデータを引用しましょう。
注文合計は以下のとおりで、全員の平均が「2,448」となっております。ここで中央値を調べると、なんと中央値が「1,650」となっており、平均との差が「800」近くあることがわかります。
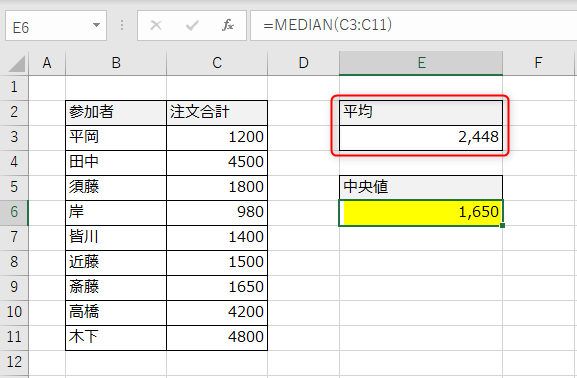
中央値を知ることで、平均とどれだけズレがあるのか? どれだけデータが散らばってしまっているのか? を簡単に把握することができるんですね。
もちろん、体重のような平均は思いっきり外れた値がないため、平均と中央値はほぼ一致します。
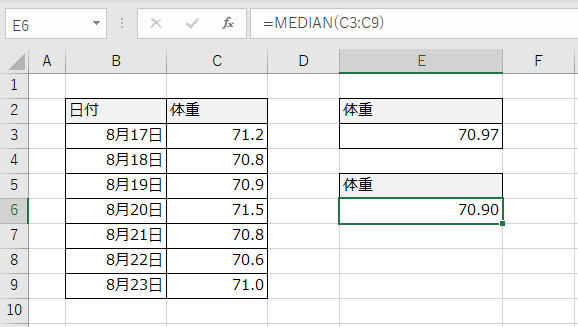
実際はヒストグラムを作成してデータ区間を示した縦棒グラフでデータを分析していくのですが、ここでは関数の説明なのでそこまでは触れません。
MEDIAN関数はAVERAGE関数のサポート役、と覚えておくといいでしょう。
関数ステータス
関数ライブラリの種類
統計
数式の構文
=MEDIAN(数値1, 数値2……)
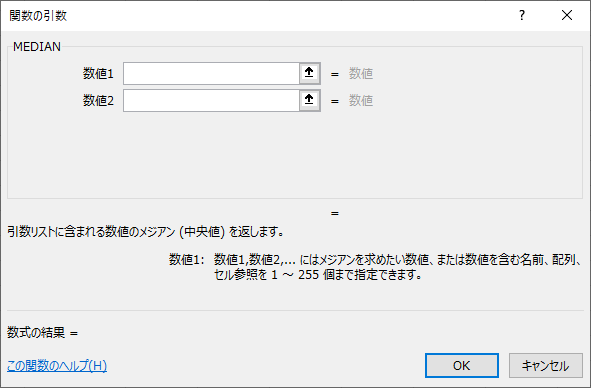
引数ダイアログ