CORREL(コリレーション)関数の使い方
CORREL(コリレーション)関数は、2つの配列データから相関係数を出力してくれる関数です。
【構文】
=CORREL(配列1, 配列2)
【使用例】
- =CORREL(B2:B100,C2:C100)
セルB2~B100までの数値データ(配列1)と、セルC2~C100までの数値データ(配列2)より、相関係数を出力します。
[char no=”1″ char=”さえちゃん1”]相関係数は必ず「-1 ~ 1」までの間で出力されます。裏側では難しい数式を使ってこの係数が計算されるのですが、正の範囲で出力された結果は「正の相関」、負の範囲で出力された結果は「負の相関」、「0」の場合は「無相関」と言います。散布図を使ったとき、点の集まりを線形で表現したときの強弱を測る指標です。[/char]
関数説明
相関係数は「 r 」で表現されます。
相関係数を出力する数式は、以下のように複雑です。
r = ( x, y の共分散 )/ ( x の標準偏差 × yの標準偏差 )
共分散についてはCOVARIANCE関数、標準偏差に関してはSTDEV関数について説明します(まだ未掲載)。以下のサンプルデータで、相関係数を求めてみましょう。
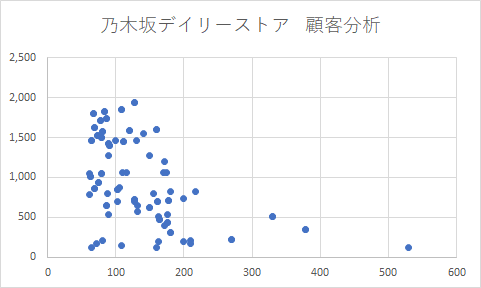
架空の店舗、乃木坂デイリーストアの分析で、滞在時間と売上金額に相関があるかどうか? この係数を調べてみます。
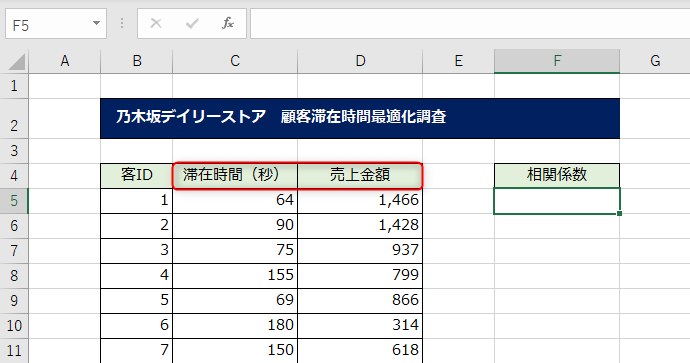
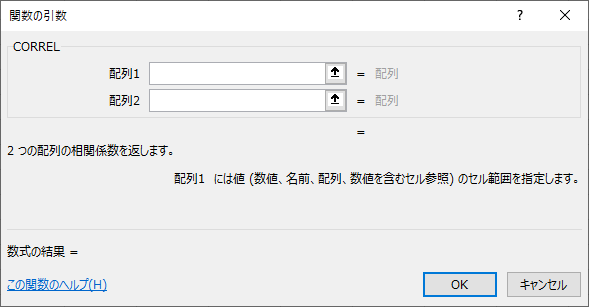
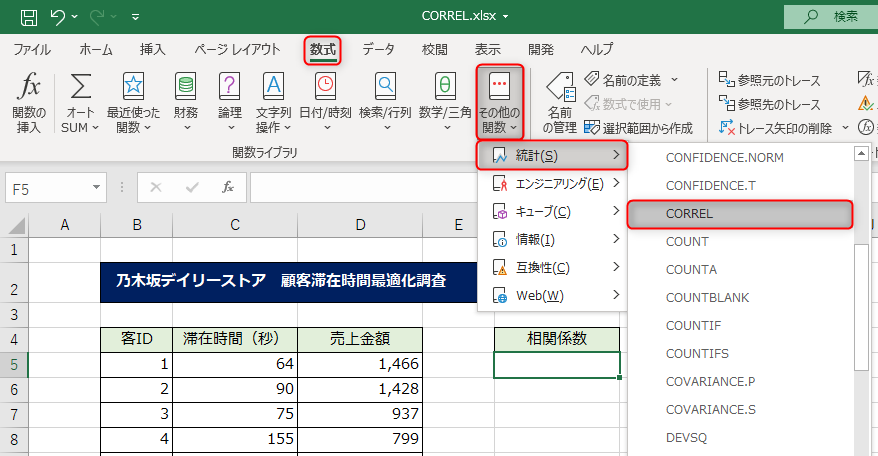
アクティブセルをF5に置きます。CORREL関数は、[数式]タブ→[その他の関数]→[統計]にあります。
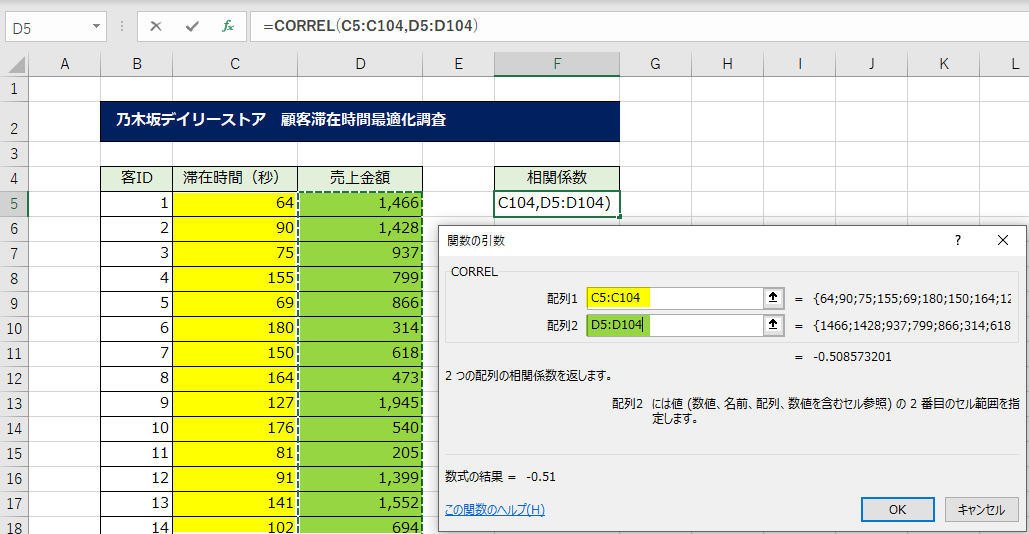
配列1は「滞在時間」の列、配列2は「売上金額」の列を選択しましょう。
相関係数は「-0.51」と出力されました。
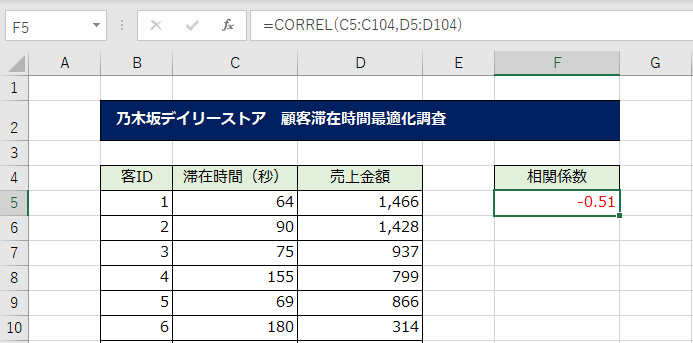
つまり、負の相関係数なので
「店舗の滞在時間が短ければ、売上金額が高い」
「店舗の滞在時間が長ければ、売上金額が低い」
というとっかかりを見つけることができました。
この相関係数は、教科書的には「0.3」おきで分類しています。
| 強い正の相関 | 0.9~0.6 |
|---|---|
| やや強い正の相関 | 0.6~0.3 |
| 弱い正の相関 | 0.3~0.1 |
| 無相関 | 0 |
| 弱い負の相関 | -0.1~-0.3 |
| やや強い負の相関 | -0.3~-0.6 |
| 強い負の相関 | -0.6~-0.9 |
相関係数は、「ピアソンの積率相関係数」「相関比」「クラメールの連関係数」「スピアマンの順位相関係数」といろいろありますが、相関係数と単にいうと「ピアソンの積率相関係数」を指します。
イギリスの数理統計学者、カール・ピアソンさんが提唱した理論ですね。CORREL関数は理論が難しいのですが、Excel上での数式作成は非常にシンプルです。
さえちゃんのCORREL関数ワンポイントアドバイス
[char no=”4″ char=”さえちゃん3”]分析業務の中で、ときどき「相関」と「因果関係」をイコールで考えてしまっている人がいますけど、全然意味が違うので注意してください。「相関があるからこういう結果になるんだ!」と決定するのは、かなり危険なことです。[/char]
相関係数は、「-0.51」だから、やや強い負の相関にある。じゃあ、店舗の滞在時間を可能な限り短くすれば、売り上げはもっと上がるはずだ!
と、相関係数から単純に因果関係を導いてしまうと、このように非常に危険な判断をしてしまいます。

相関係数による数字の裏付けができたら、この店舗における理想の滞在時間は何秒なのか? をいくつか設定し、テストを行います。
テストにはコストや時間が費やされますので、何度もできるものでもありません。しかも、テストを開始すると、すべての人間が動くので、巻き戻しができなくなります。
そのため、分析者はすべての責任を負わなければいけなくなるわけです。
そして、最適値を見つけることができたら、それが再現性があるか? を必ず確認します。再現性が認められて、初めてこれが因果関係がある、というフェーズに持ち込むことができるので、あくまで相関係数は、散布図から2つのデータの相関性を読み解くだけのツールにしかなりません。
このことをしっかり覚えておきましょう。
関数ステータス
関数ライブラリの種類
統計
数式の構文
=CORREL(配列1, 配列2)
引数ダイアログ